Understanding the Difference Between Linear and Logistic Regression Models | by Tushar Babbar | AlliedOffsets

Regression analysis is a popular statistical method used for predicting the relationship between one dependent variable and one or more independent variables. In this blog post, we will discuss the two most commonly used regression models — linear regression and logistic regression — and their differences.

Table of Contents

Linear Regression

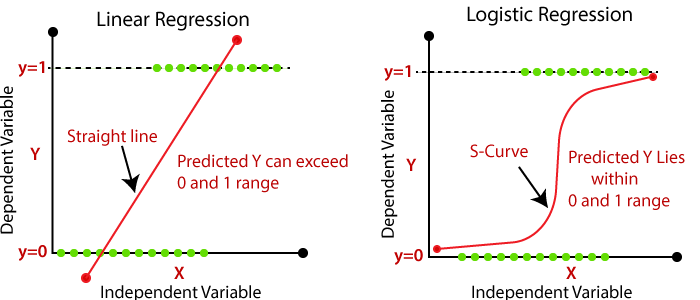
Linear regression is a regression analysis used to model the linear relationship between a dependent variable and one or more independent variables. The main goal of linear regression is to find the best-fit line through the data points that minimizes the sum of the squared residuals (the difference between the predicted value and the actual value).

Equation

The equation of a simple linear regression model is given by:

where y is the dependent variable, x is the independent variable, b0 is the intercept, and b1 is the slope coefficient. The values of b0 and b1 are estimated using the least squares method.

Advantages

Easy to interpret and understand.
Performs well when the relationship between the dependent and independent variables is linear.
Can be used for both continuous and categorical independent variables.

Disadvantages

Assumes a linear relationship between the dependent and independent variables, which may not always be true.
Sensitive to outliers.
Cannot handle categorical dependent variables.

Real-world Example

Linear regression can be used to predict the price of a house based on its size, location, and other features. By fitting a linear regression model to a dataset of historical house prices, we can estimate the relationship between the house features and the price, and use the model to predict the price of new houses.

Code Example

Here’s an example of how to implement linear regression using scikit-learn library in Python:

import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error# read and prepare the data
df = pd.read_csv('data.csv')
X = df[['independent_var']]
y = df['dependent_var']
# train the model
model = LinearRegression()
model.fit(X, y)
# make predictions and calculate metrics
y_pred = model.predict(X)
mse = mean_squared_error(y, y_pred)

Logistic Regression

Logistic regression is a regression analysis used to model the relationship between a dependent variable and one or more independent variables. Unlike linear regression, logistic regression predicts binary outcomes — either 0 or 1. The output of logistic regression is a probability value that represents the likelihood of the binary outcome.

Equation

The equation of a logistic regression model is given by:

where p is the probability of the binary outcome, z is the weighted sum of the independent variables, and e is the mathematical constant (approximately 2.71828). The values of the coefficients are estimated using maximum likelihood estimation.

Advantages

Can handle both continuous and categorical independent variables.
Performs well when the relationship between the dependent and independent variables is non-linear.
Outputs a probability value that can be used to make binary predictions.

Disadvantages

Assumes a linear relationship between the independent variables and the logarithm of the odds ratio, which may not always be true.
Requires a large sample size to estimate the coefficients accurately.
Sensitive to outliers.

Real-world Example

Logistic regression can be used to predict whether a customer will churn or not based on their demographic information and transaction history. By fitting a logistic regression model to a dataset of historical customer data, we can estimate the relationship between the customer features and their likelihood of churning, and use the model to predict the churn probability of new customers.

Code Example

Here’s an example of how to implement logistic regression using the scikit-learn library in Python:

import pandas as pd
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, classification_report# read and prepare the data
df = pd.read_csv('data.csv')
X = df[['independent_var']]
y = df['binary_dependent_var']
# train the model
model = LogisticRegression()
model.fit(X, y)
# make predictions and calculate metrics
y_pred = model.predict(X)
accuracy = accuracy_score(y, y_pred)
report = classification_report(y, y_pred)

Assumptions and Regularization

Both linear regression and logistic regression have certain assumptions that must be met for the models to be accurate. For linear regression, the main assumptions are linearity, independence, homoscedasticity, and normality. For logistic regression, the main assumptions are the linearity of independent variables and the absence of multicollinearity.

In addition, both models can benefit from regularization techniques that help to prevent overfitting and improve performance. Regularization adds a penalty term to the loss function, which discourages the model from fitting too closely to the training data.

Types of Regularization

L1 regularization (also known as Lasso regression) adds a penalty term that encourages the coefficients to be zero for some of the independent variables, effectively performing feature selection.
L2 regularization (also known as Ridge regression) adds a penalty term that shrinks the coefficients towards zero, effectively reducing their magnitude.

Code Example

Here’s an example of how to implement regularization using the scikit-learn library in Python:

import pandas as pd
from sklearn.linear_model import Lasso, Ridge# read and prepare the data
df = pd.read_csv('data.csv')
X = df[['independent_var']]
y = df['dependent_var']
# train the models with regularization
lasso_model = Lasso(alpha=0.1)
ridge_model = Ridge(alpha=0.1)
lasso_model.fit(X, y)
ridge_model.fit(X, y)
# make predictions and compare coefficients
lasso_coef = lasso_model.coef_
ridge_coef = ridge_model.coef_

Linear regression and logistic regression are two commonly used regression models that have different strengths and weaknesses. Linear regression is used for predicting continuous values, while logistic regression is used for predicting binary outcomes. Both models have assumptions that must be met for accurate predictions and can benefit from regularization techniques to prevent overfitting and improve performance.

When choosing between linear regression and logistic regression, it’s important to consider the nature of the problem and the type of outcome variable you are trying to predict. By understanding the differences between these two models, you can select the one that best suits your needs and achieve better predictions.

Thank you for taking the time to read my blog! Your feedback is greatly appreciated and helps me improve my content. If you enjoyed the post, please consider leaving a review. Your thoughts and opinions are valuable to me and other readers. Thank you for your support!